Przedział ufności dla średniej - definicja, zastosowanie i przykłady w analizie statystycznej

Przedział ufności to podstawowa koncepcja w statystyce, zapewniająca zakres wartości, które prawdopodobnie obejmują nieznany parametr populacji. Tekst ma na celu wyjaśnienie ich celu i zastosowania w analizie statystycznej. Definiując, czym są przedziały ufności i badając sposób ich obliczania, artykuł ilustruje ich znaczenie w podejmowaniu decyzji oraz badaniach. Na przykładach pokażemy, w jaki sposób przedziały ufności zapewniają miarę niepewności oraz pewności dla szacunków wartości, co czyni je nieocenionymi narzędziami dla naukowców, analityków i decydentów.

Kluczowe wnioski

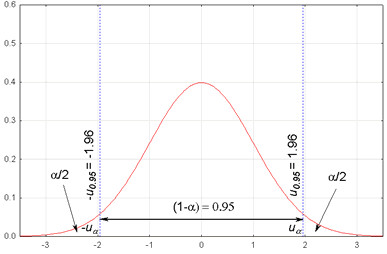
• Przedziały ufności zapewniają zakres dla parametru populacji z określonym poziomem ufności.

• Pomagają określić precyzję oszacowania i informują o niepewności.

• Przedziały ufności są kluczowym elementem podejmowania decyzji zarówno w kontekście naukowym jak i biznesowym.

Konstrukcja przedziału ufności

Przedział ufności (confidence interval) to rodzaj szacowania obliczanego na podstawie statystyk obserwowanych danych. Pozwala na określenie zakresu wartości, który uważa się za zawierający prawdziwą wartość nieznanego parametru populacji (średnia, różnica między dwiema średnimi, proporcja itp.). Przedział ufności budujemy, mając na uwadze poziom ufności - zazwyczaj 95% lub 99% - co oznacza, że jeśli ta sama populacja jest wielokrotnie próbkowana i obliczane są przedziały, prawdziwy parametr populacji będzie znajdował się w tych przedziałach odpowiednio w 95% lub 99% przypadków.

Przykład: W przypadku badania szacującego średni wzrost mężczyzn w Wielkiej Brytanii można podać, że 95% przedziału ufności wynosi od 170 cm do 180 cm. Sugerowałoby to, że istnieje 95% prawdopodobieństwo, że prawdziwa wartość parametru, czyli średni wzrost wszystkich mężczyzn w Wielkiej Brytanii, mieści się w tym przedziale.

Istotność statystyczna

Istotność statystyczna odnosi się bezpośrednio do koncepcji przedziałów ufności. Jeśli przedział ufności dla średniej różnicy lub wielkości efektu zawiera wartość zero (w przypadku różnicy) lub jeden (w przypadku proporcji), wynik nie jest uważany za istotny statystycznie na wybranym poziomie ufności. Innymi słowy, przedział ufności, który nie zawiera wartości hipotezy zerowej (zero dla różnic, jeden dla proporcji) wskazuje, że istnieje statystycznie istotna różnica lub efekt.

Przykład: Jeśli przedział ufności dla średniej różnicy między wynikami testów dwóch grup wynosi od 2 do 10 punktów, przedział nie zawiera zera. W związku z tym można stwierdzić z odpowiednim poziomem ufności, że istnieje znacząca różnica w wynikach testów między dwiema grupami.

Wzór i wskaźniki

Przedział ufności to zakres wartości, uzyskany na podstawie statystyk próby, który prawdopodobnie zawiera wartość nieznanego parametru populacji. Wzór na przedział ufności zazwyczaj obejmuje średnią z próby (x̄), margines błędu oraz odchylenie standardowe (s) lub błąd standardowy (SE). Przyjmuje on ogólną postać: CI = x̄ ± margines błędu

Parametry niezbędne do obliczeń obejmują:

• x̄: Średnia próbki

• n: Wielkość próbki

• s: Odchylenie standardowe próbki

• σ: Odchylenie standardowe całej populacji (jeśli jest znane)

• SE: Błąd standardowy średniej = s / √(n)

Ogólny wzór na przedział ufności dla średniej populacji, gdy znane jest odchylenie standardowe populacji, jest podany przez:

CI=x̄ ± (Z×SE)

gdzie x̄ to średnia z próby, Z to wartość Z ze standardowego rozkładu normalnego odpowiadająca pożądanemu poziomowi ufności (np. 1,96 dla ufności 95%), a SE to błąd standardowy średniej.

Margines błędu

Margines błędu odzwierciedla maksymalną oczekiwaną różnicę między prawdziwym parametrem populacji a oszacowaniem próby. Obejmuje on zarówno poziom ufności, jak i zmienność danych. Poziom ufności jest zwykle ustalany na 95%, chociaż inne poziomy (takie jak 90% lub 99%) mogą być również stosowane w zależności od pożądanej precyzji. Margines błędu jest obliczany za pomocą wzoru: Margines błędu = z lub t * (SE)

Gdzie:

• z lub t: Wynik z lub wynik t odpowiadający wybranemu poziomowi ufności.

• SE: błąd standardowy

Współczynniki Z i T

Wybór między wartościami z i t zależy od tego, czy znane jest odchylenie standardowe populacji oraz od wielkości próby. W przypadku próbek o dużej liczebności lub gdy znane jest odchylenie standardowe populacji, stosowany jest wynik z, który odpowiada odchyleniu standardowemu w rozkładzie normalnym. Także odwrotnie, w przypadku mniejszych próbek (n < 30) bez znanego odchylenia standardowego populacji, wynik t z rozkładu t jest bardziej odpowiedni, ponieważ dostosowuje się do dodatkowej niepewności.

Wartości krytyczne (z lub t) odpowiednie dla najbardziej powszechnych poziomów ufności to:

• 1,96 dla 95% przedziału ufności przy użyciu rozkładu z

• 2,58 dla 99% przedziału ufności przy użyciu rozkładu z

• Wartości z tabeli rozkładu t dla 95% lub 99% przedziału ufności przy użyciu rozkładu t, różniące się w zależności od stopni swobody (df = n - 1).

Dzięki tym obliczeniom badacze mogą dokonywać świadomych szacunków parametrów populacji, takich jak średnie lub proporcje, z określonym przedziale ufności.

Interpretacja przedziałów ufności

Interpretując przedziały ufności, ważne jest, aby zrozumieć, że oferują one zakres, w którym szacuje się, że mieści się prawdziwy parametr populacji, przy pewnym poziomie ufności. Granice ufności odnoszą się do dolnych i górnych granic przedziału ufności, podkreślając ich rolę w określaniu zakresu, w którym szacuje się, że mieści się prawdziwy parametr populacji. Ta sekcja poprowadzi czytelnika przez szacunki przedziałowe i poziomy ufności, aby wyjaśnić ich zastosowanie w analizie statystycznej.

Oszacowania przedziałowe

Oszacowanie przedziałowe zapewnia zakres wartości, który na podstawie danych z próby ma zawierać parametr populacji, taki jak średnia lub proporcja. Na przykład przedział ufności dla średniej wyników testu może być przedstawiony jako (100 p 2,5), gdzie 100 to średnia z próby, a 2,5 to margines błędu. Prawdziwa średnia populacji powinna mieścić się w tym przedziale.

Poziom ufności

Poziom ufności oznacza częstotliwość, z jaką przedział ufności, obliczony na podstawie wielu próbek, zawierałby prawdziwy parametr populacji. Jest on wyrażony w procentach (np. 95% lub 99%). Poziom ufności 95% sugeruje, że gdyby pobrano 100 różnych próbek i obliczono szacunki przedziałów, około 95 z tych przedziałów ufności zawierałoby prawdziwy parametr populacji.

Obliczanie przedziału ufności - przykłady

Przedziały ufności są podstawowym narzędziem statystycznym wykorzystywanym w różnych dziedzinach do szacowania wiarygodności szacunków opartych na próbach. Oferują one zakres, w którym można oczekiwać, z pewnym poziomem ufności, prawdziwego parametru populacji.

Badanie rynku - wycena produktu

Zespół ds. badań rynkowych chce ustalić idealną cenę nowego ekspresu do kawy. Ankietują 150 potencjalnych klientów i stwierdzają, że średnia gotowość do zapłaty wynosi 120 USD z odchyleniem standardowym 20 USD.

Obliczenia:

• Średnia z próby (x̄): $120

• Odchylenie standardowe (s): $20

• Wielkość próby (n): 150

• Błąd standardowy (SE):

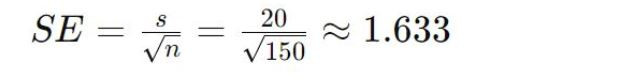
• Wartość Z dla 95% poziomu ufności: 1,96 (zastosowano rozkład normalny ze względu na duży rozmiar próby)

95% przedział ufności:

CI=xˉ±(Z×SE)=120±(1.96×1.633)

CI=120±3.2

CI=[116.8,123.2]

Przedział ten sugeruje, że firma może być w 95% pewna, że rzeczywista średnia gotowość do zapłaty za ekspres do kawy wśród wszystkich potencjalnych klientów wynosi od 116,80 USD do 123,20 USD.

Badania marketingowe - skuteczność reklamy

Zespół marketingowy prowadzi kampanię reklamową online i chce oszacować wzrost świadomości marki. Przebadano próbę 100 widzów i stwierdzono wzrost świadomości marki o 15 punktów procentowych, przy odchyleniu standardowym wynoszącym 8 punktów procentowych.

Obliczenia:

• Średnia z próby (x̄): 15%

• Odchylenie standardowe (s): 8%

• Wielkość próby (n): 100

• Błąd standardowy (SE):

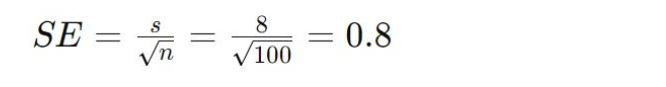
• Wartość Z dla 95% poziomu ufności: 1.96

95% przedział ufności:

CI=xˉ±(Z×SE)=15±(1.96×0.8)

CI=15±1.568

CI=[13.432,16.568]

Oznacza to, że zespół marketingowy może być w 95% pewny, że rzeczywisty wzrost świadomości marki spowodowany reklamą mieści się w przedziale od 13,432% do 16,568%.

Przykład 3: Badania UX - poprawa użyteczności strony internetowej

Zespół UX mierzy czas potrzebny użytkownikom na wykonanie określonego zadania na stronie internetowej przed i po przeprojektowaniu. Średnia poprawa czasu wykonania zadania wśród 40 użytkowników wynosi 30 sekund, z odchyleniem standardowym wynoszącym 10 sekund.

Obliczenia:

• Średnia próbki (x̄): 30 sekund

• Odchylenie standardowe (s): 10 sekund

• Wielkość próbki (n): 40

• Błąd standardowy (SE):

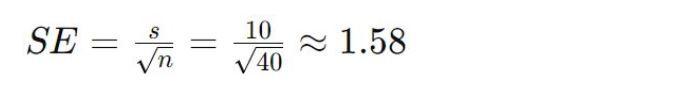
• Wartość t dla 95% ufności przy 39 stopniach swobody: około 2,02 (z tabeli rozkładu t)

95% przedział ufności:

CI = x̄ ± (t×SE)=30±(2.02×1.58)

CI=30±3.1916

CI=[26.8084,33.1916]

Ten przedział ufności wskazuje, że zespół UX może być w 95% pewny, że rzeczywista średnia poprawa czasu wykonania zadania w wyniku przeprojektowania strony internetowej wynosi od 26,8084 sekundy do 33,1916 sekundy.

Statystyczne porównanie dwóch sloganów reklamowych

Rozważmy przykład marketingowy, w którym firma testuje dwa różne slogany reklamowe, aby określić, który z nich skuteczniej rezonuje z odbiorcami. Firma zmierzy wpływ tych sloganów na intencje zakupowe konsumentów za pomocą ankiety.

• Slogan A: Przetestowany na 250 konsumentach, 130 wskazało, że zwiększył ich intencje zakupowe.

• Slogan B: Przetestowany na 250 konsumentach, 150 wskazało, że zwiększył ich zamiar zakupu.

Określ, czy istnieje statystycznie istotna różnica w skuteczności obu sloganów na podstawie odpowiedzi konsumentów.

• Slogan A: 130 z 250 konsumentów odpowiedziało pozytywnie.

• Slogan B: 150 z 250 konsumentów odpowiedziało pozytywnie.

Obliczenia:

Proporcje

• Slogan A

• Slogan B

Błąd standardowy proporcji dla każdego ze sloganów:

• Slogan A

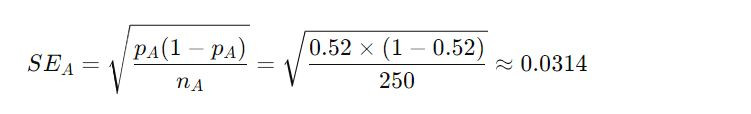
• Slogan B

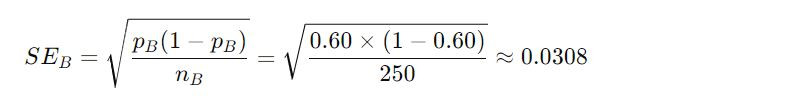
95% przedział ufności dla każdego sloganu (przy użyciu wartości Z równej 1,96 dla 95% ufności):

• Slogan A

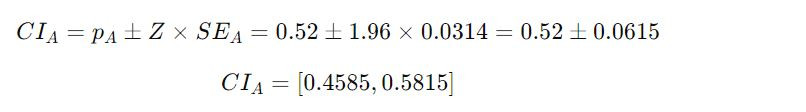
• Slogan B

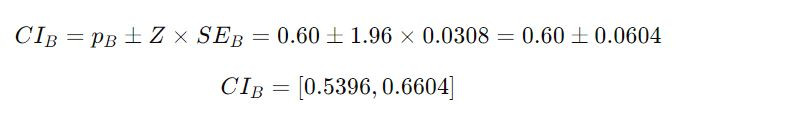
Analiza:

• Przedział ufności sloganu A: 0,4585 do 0,5815

• Przedział ufności dla sloganu B: 0,5396 do 0,6604

Przedziały ufności dla sloganu A (0,4585 do 0,5815) i sloganu B (0,5396 do 0,6604) pokrywają się. Dlatego różnica między tymi dwoma hasłami pod względem zwiększania intencji zakupu nie jest statystycznie istotna. To nakładanie się wskazuje, że dane nie dostarczają mocnych dowodów na korzyść jednego sloganu nad drugim w oparciu o badaną próbę.

Ten szczegółowy przykład pokazuje, w jaki sposób przedziały ufności mogą być wykorzystywane w badaniach klientów do statystycznej oceny istotności różnic w proporcjach, oferując jasny wgląd w preferencje klientów.

Rodzaje przedziałów ufności

Przedziały ufności występują w różnych formach, aby dostosować się do różnych zadań statystycznych. Są one niezbędnymi narzędziami w statystyce inferencyjnej, zapewniając zakres, w którym można oczekiwać znalezienia parametru populacji z pewnym stopniem pewności. Rozumienie 'wariancji populacji' jest kluczowe przy konstruowaniu przedziałów ufności, szczególnie gdy szacujemy parametry populacji, takie jak średni poziom wody w rzece czy średnie miesięczne wydatki na kulturę i sport. „Górna granica” przedziału ufności ma kluczowe znaczenie dla określenia najwyższej wartości w zakresie, który może zawierać parametr populacji, odgrywając kluczową rolę w obliczeniach statystycznych dla parametrów takich jak σ2 lub średnia populacji, a także w określaniu zakresów dla ryzyka względnego i współczynnika szansy.

Przedział dla jednej próby

Przedział ufności dla jednej próby jest używany, gdy chcemy oszacować parametr populacji na podstawie pojedynczej próby. Zazwyczaj stosuje się go do oszacowania średniej lub proporcji, gdy badana jest tylko jedna grupa. Na przykład, jeśli badanie ma na celu oszacowanie średniego wzrostu dorosłych kobiet w mieście, naukowcy wykorzystają dane z pojedynczej losowej próby kobiet do skonstruowania przedziału.

Przedział dla dwóch prób

Z kolei przedział ufności dla dwóch prób porównuje różnicę między dwiema niezależnymi grupami. Ten rodzaj przedziału ufności jest szczególnie przydatny, gdy celem jest porównanie średnich z dwóch różnych grup. Na przykład porównanie średniego skurczowego ciśnienia krwi między palaczami i osobami niepalącymi wymaga oszacowania różnicy średnich z dwóch oddzielnych prób, co prowadzi do przedziału ufności dla dwóch prób.

Przedział ufności a testowanie hipotez

Zrozumienie różnicy między przedziałem ufności a testowaniem hipotez jest niezbędne do dokładnej interpretacji wyników statystycznych. Obie metody oferują różny wgląd w parametry populacji w oparciu o dane próbne.

Porównanie

Przedział ufności określa zakres wartości, w którym badacze mogą stwierdzić z określonym poziomem pewności, że parametr populacji się znajduje. Na przykład 95% przedział ufności dla średniej populacji mówi nam, że jeśli ta sama populacja jest wielokrotnie próbkowana i obliczane są przedziały, około 95% z nich zawiera prawdziwą średnią populacji.

Z drugiej strony, testowanie hipotez służy do oceny dowodów przeciwko hipotezie zerowej, domyślnemu stwierdzeniu, że nie istnieje żaden efekt lub różnica. Ten test daje wartość p, która wskazuje prawdopodobieństwo zaobserwowania przykładowych danych lub czegoś bardziej ekstremalnego, przy założeniu, że hipoteza zerowa jest prawdziwa.

Kiedy stosować poszczególne metody

Badacze używają przedziału ufności, gdy są zainteresowani oszacowaniem zakresu, w którym mieści się parametr populacji. Jest to korzystne dla zrozumienia precyzji oszacowania i związanego z nim stopnia niepewności.

Testowanie hipotez jest bardziej odpowiednie, gdy badacze chcą podjąć decyzję lub przetestować konkretne twierdzenie dotyczące parametru populacji. Mogą oni chcieć ustalić, czy obserwowane dane próbne dostarczają wystarczających dowodów, aby odrzucić hipotezę zerową, czy też nie.

Obie metody są integralną częścią statystyki wnioskowania, ale służą różnym celom i dostarczają różnych rodzajów informacji. Jasne zrozumienie, kiedy i jak stosować te techniki, ma kluczowe znaczenie dla przeprowadzania solidnych analiz statystycznych.

Wyzwania związane z konstruowaniem przedziałów ufności

Konstruowanie przedziałów ufności wymaga precyzyjnych obliczeń i rozważań. Niezależnie od jasności teoretycznej, praktycy mogą napotkać kilka wyzwań, szczególnie w przypadku rozkładów danych odbiegających od normalnego i obsługi małych rozmiarów próbek.

Dane odbiegające od rozkładu normalnego

Gdy dane nie mają rozkładu normalnego, ustalenie przedziału ufności staje się bardziej złożone. Tradycyjne metody konstruowania przedziałów ufności często opierają się na założeniu, że dane zawierają się w rozkładzie normalnym. Jeśli to założenie zostanie naruszone, wynikowy przedział może być niedokładny. Na przykład, w przypadku danych skośnych, zwłaszcza jeśli są one silnie skośne, zwykłe parametry do obliczania przedziałów, takie jak średnia i odchylenie standardowe, mogą nie zapewniać prawdziwego odzwierciedlenia tendencji centralnej i zmienności danych.

Naukowcy opracowali alternatywne techniki radzenia sobie z takimi scenariuszami, w tym zastosowanie metod nieparametrycznych. Metody te nie opierają się na normalnym rozkładzie danych, często obejmując techniki takie jak bootstrapping, w których próbki są powtarzalnie pobierane z zestawu danych z zastąpieniem w celu utworzenia rozkładu oszacowania.

Małe liczebności prób

Małe liczebności prób stanowią kolejne wyzwanie w dokładnym obliczaniu przedziałów ufności. Przy ograniczonej liczbie obserwacji centralne twierdzenie graniczne nie ma pełnego zastosowania, co zapewnia, że przy wystarczająco dużej liczebności próby rozkład próbkowania średniej będzie rozkładem normalnym. W takich przypadkach zwykły wynik ( z ), który jest wykorzystywany do konstruowania przedziałów ufności dla dużych prób, staje się niewiarygodny i może prowadzić do przedziałów, które nie wychwytują skutecznie parametru populacji.

Radzenie sobie z małymi rozmiarami próbek często wiąże się z wykorzystaniem rozkładu ( t ), który dostosowuje się do zwiększonej zmienności nieodłącznie związanej z mniejszymi próbkami. Stopnie swobody, powiązane z wielkością próby, stają się kluczowe przy określaniu odpowiednich wartości ( t ) do wykorzystania. Może to być bardziej skuteczne niż przybliżenie normalne, zapewniając bardziej wiarygodne oszacowanie przedziałów ufności dla małych rozmiarów próbek.

Często zadawane pytania

Ta sekcja zawiera odpowiedzi na najczęściej zadawane pytania dotyczące koncepcji i wykorzystania przedziałów ufności w analizie statystycznej.

Czym jest przedział ufności w analizie statystycznej?

Przedział ufności w analizie statystycznej to zakres wartości, który prawdopodobnie zawiera prawdziwą wartość parametru populacji. Zapewnia on oszacowanie stopnia niepewności związanego ze statystyką próby.

Jak oblicza się i interpretuje 95% przedział ufności?

95% przedział ufności jest obliczany przy użyciu błędu standardowego średniej i wartości krytycznej z rozkładu, która odpowiada pożądanemu poziomowi ufności. Aby zinterpretować ten przedział, można powiedzieć, że z 95% pewnością prawdziwy parametr populacji leży w tym zakresie.

W jaki sposób przedziały ufności są stosowane w praktyce?

Przedziały ufności są stosowane w różnych praktycznych sytuacjach, takich jak badania medyczne w celu oszacowania skuteczności leku, w testach jakości w celu określenia niezawodności produktu lub w badaniach ankietowych w celu oceny opinii publicznej ze znanym marginesem błędu.

Jakie są trzy powszechnie stosowane poziomy ufności w testach istotności statystycznej?

Trzy powszechnie stosowane poziomy ufności w testach istotności statystycznej to 90%, 95% i 99%. Te poziomy ufności odpowiadają prawdopodobieństwu, że prawdziwy parametr istnieje w obliczonym przedziale.

Co oznacza termin „poziom ufności” w kontekście wnioskowania statystycznego?

Termin „poziom ufności” w kontekście wnioskowania statystycznego określa ilościowo prawdopodobieństwo, że obliczony przedział ufności faktycznie zawiera prawdziwy parametr populacji. Poziom ten odzwierciedla częstotliwość, z jaką przedział uchwyciłby parametr, gdyby to samo badanie zostało wielokrotnie powtórzone w tych samych warunkach.