Mediana - definicja i przykłady użycia: Zrozumienie tendencji centralnej w statystyce

Czym jest mediana?

Mediana jest ważnym pojęciem w statystyce, zapewniającym sposób na znalezienie środkowej wartości w zbiorze danych. Aby obliczyć medianę, należy uporządkować dane i znaleźć wartość środkową lub uśrednić dwie wartości środkowe, jeśli liczba punktów danych jest parzysta.

W przeciwieństwie do średniej arytmetycznej, na którą mogą wpływać wartości skrajne, mediana jest miarą tendencji centralnej, która pozostaje stabilna nawet w przypadku występowania wartości odstających i nietypowych.

Sprawia to, że jest to cenne narzędzie do zrozumienia rozkładów danych, które są wypaczone lub mają nietypowe wartości.

Definicja mediany

• Mediana to wartość środkowa zbioru danych uporządkowanych rosnąco lub malejąco.

• Wartość mediany jest miarą tendencji centralnej, która oddziela wyższą połowę od niższej połowy danych.

• Mediana jest rzetelną miarą tendencji centralnej, która nie jest zniekształcona przez wartości skrajne.

Znaczenie mediany w statystyce

• Mediana jest często używana jako lepsza reprezentacja środka rozkładu niż średnia.

• Jest to popularna metoda podsumowująca w statystyce opisowej.

• Mediana służy do identyfikacji centralnej pozycji zestawu danych. Jest ona szczególnie przydatna w zestawach danych z danymi skośnymi, ponieważ wartości skrajne mają na nią mniejszy wpływ.

Zrozumienie punktów danych

Czym są punkty danych?

Punkty danych to indywidualne wartości lub obserwacje w zestawie danych, które reprezentują określone pomiary lub charakterystyki. Każdy punkt danych dostarcza informacji, które w połączeniu z innymi pomagają stworzyć pełny obraz analizowanych danych. Punkty te mają fundamentalne znaczenie w analizie statystycznej i mogą się znacznie różnić w zależności od kontekstu badania.

Można je sklasyfikować jako ilościowe lub jakościowe, służące różnym celom w analizie danych.

Rodzaje punktów danych

Ilościowe punkty danych:

• Definicja: Ilościowe punkty danych to wartości liczbowe, które określają coś ilościowo. Są mierzalne i mogą być używane do wykonywania operacji arytmetycznych.

• Przykłady: Wysokość, waga, temperatura, wiek, dane dotyczące sprzedaży lub dowolna liczba policzalna.

• Zastosowania: Te punkty danych są często wykorzystywane w analizach statystycznych w celu znalezienia średnich, median, trendów i korelacji. Pomagają w generowaniu spostrzeżeń poprzez obliczenia matematyczne i reprezentacje graficzne.

Jakościowe punkty danych:

• Definicja: Jakościowe punkty danych to wartości kategoryczne, które opisują atrybuty lub cechy. Są one nienumeryczne i dostarczają informacji opisowych.

• Przykłady: Kolory, nazwy, etykiety, rodzaje produktów, opinie klientów i odpowiedzi na ankiety.

• Zastosowania: Te punkty danych są wykorzystywane do klasyfikowania i kategoryzowania danych, pomagając w zrozumieniu wzorców, preferencji i trendów w kontekstach nienumerycznych. Są one niezbędne w dziedzinach takich jak badania rynku i nauki społeczne, gdzie zrozumienie jakości i charakteru danych ma kluczowe znaczenie.

Wyznaczanie mediany

Mediana jest kluczową miarą w statystyce, która reprezentuje wartość środkową zestawu danych. Dzieli ona dane na dwie równe połowy, gdzie połowa punktów danych znajduje się poniżej mediany, a połowa powyżej niej, czyli liczba środkowa to wartość, która dzieli zestaw danych na dwie równe połowy. Obliczanie mediany zależy od tego, czy liczba punktów danych w zestawie jest nieparzysta czy parzysta.

Mediana nieparzystej liczby punktów danych

Gdy liczba punktów danych jest nieparzysta, mediana jest łatwa do określenia. Jest to po prostu wartość, która znajduje się w środku uporządkowanego zestawu danych.

Przykład: Rozważmy zestaw danych 1, 3, 5, 7, 9.

• Krok 1: Uporządkuj dane w kolejności rosnącej (w tym przypadku dane są już uporządkowane).

• Krok 2: Zidentyfikuj wartość środkową.

• Mediana to wartość środkowa, która w tym przypadku wynosi 5.

Metoda ta zapewnia, że mediana dzieli zestaw danych na dwie równe części, przy czym jedna część ma wartości mniejsze niż mediana, a druga część ma wartości większe niż mediana.

Mediana parzystej liczby punktów danych

Gdy liczba punktów danych jest parzysta, nie ma jednej wartości środkowej. Zamiast tego medianę oblicza się, biorąc średnią arytmetyczną z dwóch wartości środkowych.

Przykład: Rozważmy zestaw danych 1, 3, 5, 7, 9, 11.

• Krok 1: Uporządkuj dane w kolejności rosnącej (w tym przypadku dane są już uporządkowane).

• Krok 2: Zidentyfikuj dwie środkowe wartości, którymi są 5 i 7.

• Krok 3: Oblicz średnią z tych dwóch wartości środkowych.

• Mediana wynosi (5 + 7) / 2 = 6.

Obliczanie mediany

Medianę można obliczyć przy użyciu różnych metod w zależności od tego, czy dane są niezgrupowane czy zgrupowane. Oto jak określić medianę dla obu typów zestawów danych:

Wzór dla danych niezgrupowanych

W przypadku danych niezgrupowanych medianę można znaleźć za pomocą prostego wzoru. Wzór ten zakłada, że zestaw danych jest uporządkowany od najmniejszego do największego.

Wzór:

gdzie n to liczba punktów danych. W przypadku parzystej liczby obserwacji mediana jest znajdowana poprzez uśrednienie dwóch wartości środkowych.

Przykład: Rozważmy zestaw danych 1, 2, 3, 4, 5.

n = 5

Mediana to trzecia wartość w uporządkowanym zestawie danych, czyli 3.

Wzór dla danych pogrupowanych

W przypadku danych pogrupowanych mediana jest obliczana przy użyciu bardziej złożonego wzoru, który uwzględnia przedziały klasowe i ich częstotliwości.

Wzór:

gdzie:

• l = dolna granica klasy mediany

• n = całkowita liczba punktów danych

• cf = skumulowana częstotliwość klasy przed klasą medianową

• f = częstotliwość klasy mediany

• h = szerokość przedziału klasowego

Przykład danych pogrupowanych:

Weźmy pod uwagę następujące pogrupowane dane:

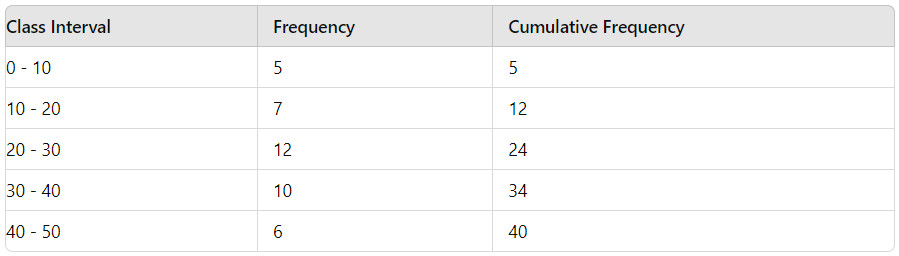
• Całkowita liczba punktów danych n = 40

• Klasa mediany: Klasa, w której skumulowana częstotliwość osiąga lub przekracza n/2 = 20

• Klasa mediany to 20-30 (ponieważ skumulowana częstotliwość do 10-20 wynosi 12, a dodanie częstotliwości 20-30 daje 24, co przekracza 20).

• l (dolna granica klasy mediany)= 20

• cf (skumulowana częstotliwość przed klasą medianową) = 12

• f (częstotliwość klasy mediany) = 12

• h (szerokość przedziału klasowego) = 10

Korzystając ze wzoru:

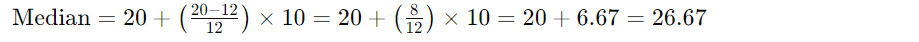
Zatem mediana wynosi około 26,67

Wyzwania związane z medianą

Mediana oferuje wiele zalet, ale wiążą się z nią też wyzwania. Wyzwania te często wynikają z ograniczeń w jej stosowaniu i jej zachowania w rozkładach skośnych.

Ograniczenia:

• Mediana może być mniej przydatna, gdy mamy do czynienia z małymi zestawami danych. W małych próbkach niewielkie zmiany w pojedynczym punkcie danych mogą znacząco przesunąć medianę. Na przykład w zestawie 5 wartości zmiana jednej liczby może zmienić medianę bardziej drastycznie niż w przypadku zestawu 50 wartości.

• Mediana nie wykorzystuje wszystkich wartości danych w swoich obliczeniach.

• W przeciwieństwie do średniej arytmetycznej, która uwzględnia każdy punkt danych, mediana analizuje tylko środkową wartość (wartości). Może to spowodować utratę informacji o rozkładzie zbioru danych.

• Brak możliwości wykorzystania jej w dalszych obliczeniach matematycznych. Podczas gdy średnią można łatwo włączyć do wzorów i testów statystycznych, medianie brakuje tej elastyczności. Sprawia to, że jest ona mniej przydatna w różnych modelach i algorytmach statystycznych.

Rozkłady skośne

W rozkładach skośnych mediana ma zarówno mocne jak i słabe strony. Pozostaje niezawodną miarą tendencji centralnej, gdy dane są silnie skośne, ponieważ nie mają na nią wpływu wartości skrajne.

Na przykład w danych dotyczących dochodów, które obejmują osoby o bardzo wysokich zarobkach, mediana zapewnia bardziej reprezentatywną wartość centralną niż średnia. Jednak interpretacja mediany w rozkładach skośnych może być czasami myląca.

Chociaż poprawnie identyfikuje wartość środkową, nie odzwierciedla zakresu skośności. Na przykład, dwa zbiory danych mogą mieć tę samą medianę, ale znacznie różne rozrzuty i kształty.

Wybór mediany w rozkładach skośnych może również przeoczyć znaczące wartości odstające. Wartości odstające nie mają wpływu na medianę, więc ważne trendy lub anomalie w rozkładzie danych mogą zostać pominięte lub niedostatecznie reprezentowane.

Zastosowanie mediany

Przykłady zastosowania mediany w świecie rzeczywistym

Rozkłady dochodów:

• Zastosowanie: Tak jak już wspomniano mediana jest często używana do reprezentowania rozkładów dochodów w badaniach ekonomicznych. Ponieważ dane dotyczące dochodów są zazwyczaj wypaczone przez niewielką liczbą bardzo wysokich dochodów, średnia może być myląca.

• Przykład: Rządy i ekonomiści używają mediany dochodu, aby lepiej zrozumieć typowy dochód populacji, unikając zniekształceń spowodowanych przez osoby o bardzo wysokich dochodach. Na przykład, podczas raportowania dobrobytu ekonomicznego społeczności, mediana dochodów zapewnia jaśniejszy obraz typowego doświadczenia niż średni dochód.

Badania marketingowe:

• Zastosowanie: W badaniach rynkowych mediana jest wykorzystywana do analizy zachowań i preferencji konsumentów. Pomaga w zrozumieniu tendencji centralnej odpowiedzi ankietowych, kwot zakupów lub innych mierzalnych atrybutów.

• Przykład: Marketerzy wykorzystują medianę do określenia typowych wydatków klientów na dany produkt. Jeśli kilku klientów dokonuje bardzo dużych zakupów, podczas gdy większość dokonuje mniejszych, mediana kwoty wydatków zapewnia dokładniejsze przedstawienie typowych zachowań klientów niż średnia.

Edukacja:

• Zastosowanie: W edukacji mediana jest używana do określenia mediany wyników uczniów, co pomaga zrozumieć typowe wyniki grupy uczniów bez wpływu na wyjątkowo wysokie lub niskie wyniki.

• Przykład: Szkoły i badacze edukacyjni wykorzystują medianę wyników w standardowych testach, aby ocenić typowy poziom wyników uczniów. Jest to szczególnie przydatne w dużych klasach lub okręgach, gdzie kilka bardzo wysokich lub bardzo niskich wyników może wypaczyć średnią.

Mediana w ujęciu graficznym

Zrozumienie mediany za pomocą wykresów, takich jak histogramy i wykresy pudełkowe, może pomóc w wizualizacji tendencji centralnej danych. Te narzędzia wizualne wyjaśniają, w jaki sposób mediana odnosi się do zestawu danych.

Mediana na histogramach

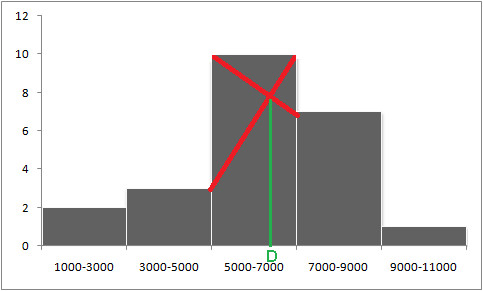
Histogramy przedstawiają rozkład danych za pomocą słupków, z których każdy reprezentuje częstotliwość wartości w danym zakresie. Medianę można znaleźć, identyfikując punkt, w którym połowa danych znajduje się poniżej, a połowa powyżej.

W przypadku rozkładu symetrycznego, takiego jak wzrost kobiet w college'u, mediana pokrywa się ze średnią i modą, często w środku histogramu.

W rozkładach skośnych mediana zapewnia lepszą wartość centralną niż średnia, ponieważ nie ma na nią wpływu wartość ekstremalna. Korzystanie z histogramów umożliwia łatwą wizualną identyfikację mediany poprzez pokazanie skumulowanej częstotliwości.

Wykresy pudełkowe

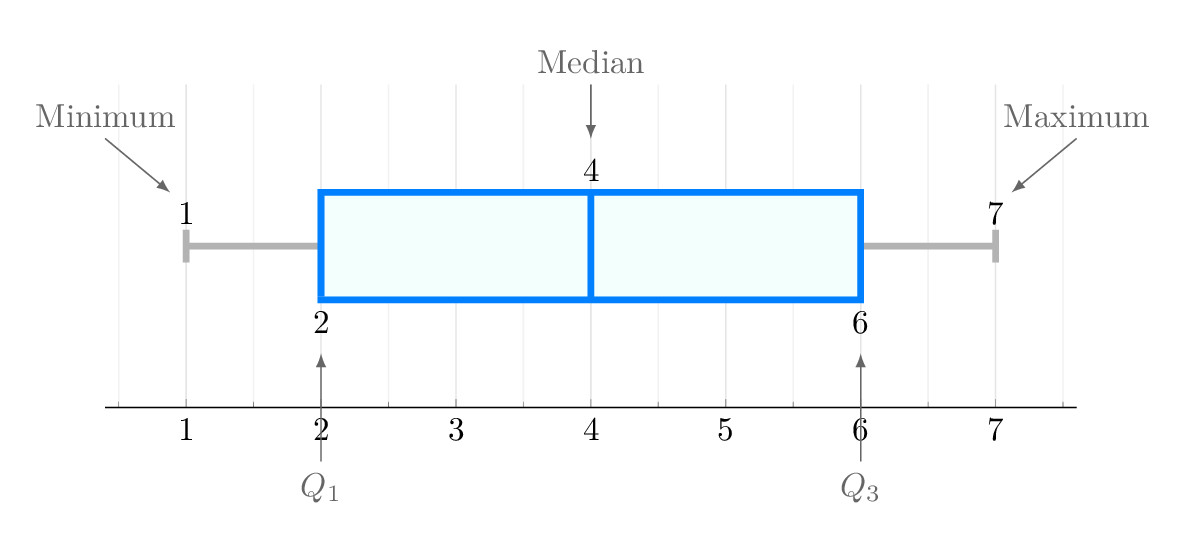
Wykresy pudełkowe lub wykresy skrzynkowe prezentują dane poprzez wyświetlanie ich rozkładu w kwartylach. Mediana jest linią wewnątrz pudełka, która dzieli je na dwie części.

Samo pudełko pokazuje zakres międzykwartylowy (IQR), od pierwszego (Q1) do trzeciego kwartyla (Q3).

Ta graficzna reprezentacja podkreśla wartości odstające i rozrzut danych.

W rozkładach skośnych linia mediany może znajdować się poza środkiem, wskazując na skośność.

Wykresy pudełkowe pomagają wizualnie porównać mediany w różnych zestawach danych lub grupach, co czyni je potężnym narzędziem do porównywania różnic między rozkładami.

Związek między średnią arytmetyczną, medianą i dominantą

Jak powiązana jest średnia arytmetyczna, mediana i dominantą?

Średnia arytmetyczna, mediana i dominanta to miary tendencji centralnej używane do podsumowania danych, z których każda zapewnia inny wgląd w zestaw danych. Zrozumienie relacji między tymi miarami jest niezbędne do analizy danych.

Przykłady średniej, mediany i dominanty

Rozkłady symetryczne: W idealnie symetrycznym rozkładzie (np. rozkładzie normalnym) średnia, mediana i dominanta są równe.

Średnia = Mediana = Dominanta

Rozkłady skośne: W rozkładach skośnych średnia, mediana i dominanta zazwyczaj nie pokrywają się.

• Dodatnio skośny (prawostronnie skośny): Średnia jest większa niż mediana, która jest większa niż dominanta.

  Dominanta < Mediana < Średnia arytmetyczna

• Ujemnie skośny (lewostronnie skośny): Średnia jest mniejsza niż mediana, która jest mniejsza niż dominanta.

  Średnia arytmetyczna < Mediana < Dominanta

Zrozumienie tych zależności pomaga zidentyfikować charakter rozkładu danych i wybrać odpowiednią miarę tendencji centralnej do analizy.

Pojęcia zaawansowane

W tej sekcji przedstawiamy, w jaki sposób mediana może być stosowana w bardziej złożonych scenariuszach, takich jak wielowymiarowa analiza danych i uogólnione ustawienia, zapewniając głębszy wgląd w jej praktyczne zastosowania.

Mediana wielowymiarowa

Mediana wielowymiarowa rozszerza pojęcie mediany na wiele wymiarów. Identyfikuje ona centralny punkt w wielowymiarowej przestrzeni, na przykład w zbiorze danych z wieloma zmiennymi.

Jedną z powszechnych metod znajdowania tej mediany jest mediana geometryczna. Punkt ten minimalizuje sumę odległości do wszystkich innych punktów w zbiorze danych, w przeciwieństwie do mediany jednowymiarowej, która uwzględnia tylko jeden wymiar.

Ważną właściwością mediany geometrycznej jest jej odporność na wartości odstające. Jeśli punkty danych są rozłożone nierównomiernie, mediana geometryczna zapewnia dokładniejszą lokalizację centralną niż średnia arytmetyczna.

Zastosowania mediany wielowymiarowej obejmują grupowanie i wykrywanie wartości odstających w danych wielowymiarowych.

Uogólnienia

Istnieje kilka sposobów na uogólnienie pojęcia mediany poza podstawowe zbiory danych. Jednym z powszechnych uogólnień jest mediana ważona, w której każdemu punktowi danych przypisywana jest waga.

Ważona mediana dzieli dane w taki sposób, że suma wag jest zrównoważona po obu stronach. Koncepcja ta jest przydatna w kontekstach, w których niektóre punkty danych są bardziej znaczące niż inne, na przykład w ważonych systemach głosowania lub modelach finansowych.

Innym uogólnieniem jest algorytm mediany median, który skutecznie znajduje przybliżoną medianę w dużych zbiorach danych. Algorytm ten działa poprzez podzielenie zbioru danych na mniejsze grupy, znalezienie mediany każdej grupy, a następnie określenie mediany tych median. Metoda ta jest szczególnie przydatna w scenariuszach wymagających szybkich i przybliżonych rozwiązań.